Описание
Задание по дисциплине «Экономико-математические методы»
Задача 1
Поставить задачу линейного программирования и найти оптимальное решение в ситуации: «Грузоперевозчик покупает автомобили. Бюджет покупки – 150 д.е. Цена 3-тонного автомобиля составляет 4 д.е., 5-тонного – 5 д.е. Возможности грузоперевозчика по техническому обслуживанию автомобилей – не более 20 единиц 3-тонных автомобилей сразу и не более 18 единиц 5-тонных. Сколько и каких автомобилей купить для обеспечения максимальной суммарной грузоподъемности автопарка».
Задача 2
Для прямой задачи линейного программирования составить двойственную. Найти оптимальные решения задач.
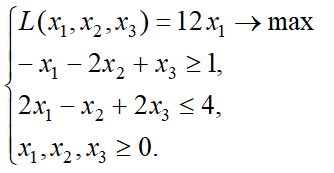
Задача 3
Составить математическую модель, найти оптимальный план перевозок и оптимальные издержки в транспортной задаче, заданной таблицами.
| Транспортные издержки на маршруте на единицу груза | |||||||||
| Поставщик | а i | Потребитель | b j | j=1 | j=2 | j=3 | |||
| i=1 | 90 | j=1 | 140 | i=1 | 2 | 5 | 2 | ||
| i=2 | 400 | j=2 | 300 | i=2 | 4 | 1 | 5 | ||
| i=3 | 110 | j=3 | 160 | i=3 | 3 | 6 | 8 | ||
Задача 4.
Составить математическую модель, найти оптимальный план перевозок и оптимальные издержки в транспортной задаче, заданной таблицами.
| Транспортные издержки на маршруте на единицу груза | |||||||||
| Поставщик | а i | Потребитель | b j | j=1 | j=2 | j=3 | |||
| i=1 | 100 | j=1 | 190 | i=1 | 4 | 2 | 1 | ||
| i=2 | 200 | j=2 | 120 | i=2 | 1 | 5 | 3 | ||
| i=3 | 70 | j=3 | 10 | i=3 | 1 | 2 | 6 | ||
Задача 5.
Составить математическую модель и найти оптимальный план назначений в задаче о назначениях, заданной таблицей.
Прибыль от назначения i-кандидата на j-должность
| Должности | ||||
| j=1 | j=2 | j=3 | ||
| кандидаты | i=1 | 3 | 7 | 5 |
| i=2 | 2 | 4 | 4 | |
| i=3 | 4 | 7 | 2 | |



