Описание
Номер билета студент определяет в соответствии с заглавной буквой фамилии.
| 1 | А | 14 | О |
| 2 | Б | 15 | П |
| 3 | В | 16 | Р |
| 4 | Г | 17 | С |
| 5 | Д | 18 | Т |
| 6 | Е- Ё | 19 | У |
| 7 | Ж | 20 | Ф или Ш |
| 8 | З | 21 | X или Щ |
| 9 | И- Й | 22 | Ц или Ы |
| 10 | К | 23 | Ч или Э |
| 11 | Л | 24 | Ц или Ю |
| 12 | М | 25 | Ч или Я |
| 13 | Н |
Оценка «неудовлетворительно» предполагает грубые ошибки при решении обеих задач или отсутствие правильного решения.
Оценка «удовлетворительно» предполагает верное решение хотя бы одной из задач.
Оценка «хорошо» предполагает верное решение обеих задач, при этом имеются отдельные погрешности в решении не повлиявшие на конечный результат.
Оценка «отлично» предполагает верные ответы на вопросы задания и корректные выводы по результатам решения задач
Ответы на билеты должны быть представлены в виде решения задач в табличном процессоре «MicrosoftExcel».
Титульный лист см. Приложение 1.
Билет №1
- Особенности статистической оценки взаимосвязи двух временных рядов.
Задача №1.Имеются эмпирические данные о банковских вкладах- Z и уровне доходов V по 20 территориям государства. Построить регрессию Z на V (использовать линейную и логарифмическую модели.
| V | 5.8 | 6.14 | 6.64 | 6.85 | 8.11 | 8.47 | 9.09 | 9.23 | 9.59 | 9.96 |
| Z | 11.8 | 12.2 | 13.1 | 14.4 | 17.5 | 18.6 | 19.1 | 19.3 | 19.8 | 18.4 |
| V | 1.01 | 1.15 | 1.91 | 2.47 | 2.66 | 2.74 | 2.93 | 4.04 | 4.50 | 4.64 |
| Z | 11.8 | 12.2 | 13.1 | 14.4 | 17.5 | 18.6 | 19.1 | 19.3 | 19.8 | 18.4 |
Выбрать наиболее адекватную модель и обосновать свой выбор
Задача №2. По 20 предприятиям региона изучается зависимость выработки продукции на одного работника (тыс. руб.) от ввода в действие новых основных фондов ( от стоимости фондов на конец года) и от удельного веса рабочих высокой квалификации в общей численности рабочих ( ).
| Номер предприятия | Номер предприятия | ||||||
| 1 | 7,0 | 3,9 | 10,0 | 11 | 9,0 | 6,0 | 21,0 |
| 2 | 7,0 | 3,9 | 14,0 | 12 | 11,0 | 6,4 | 22,0 |
| 3 | 7,0 | 3,7 | 15,0 | 13 | 9,0 | 6,8 | 22,0 |
| 4 | 7,0 | 4,0 | 16,0 | 14 | 11,0 | 7,2 | 25,0 |
| 5 | 7,0 | 3,8 | 17,0 | 15 | 12,0 | 8,0 | 28,0 |
| 6 | 7,0 | 4,8 | 19,0 | 16 | 12,0 | 8,2 | 29,0 |
| 7 | 8,0 | 5,4 | 19,0 | 17 | 12,0 | 8,1 | 30,0 |
| 8 | 8,0 | 4,4 | 20,0 | 18 | 12,0 | 8,5 | 31,0 |
| 9 | 8,0 | 5,3 | 20,0 | 19 | 14,0 | 9,6 | 32,0 |
| 10 | 10,0 | 6,8 | 20,0 | 20 | 14,0 | 9,0 | 36,0 |
- С помощью метода наименьших квадратов (МНК) оценить параметры линейной модели вида y= a0+a1x1+a2x2+e , влияния возраста и стажа работы на среднемесячную зарплату;
- Рассчитать коэффициент детерминации
Билет №2
- Оценивание параметров уравнения регрессии при наличии автокорреляции в остатках. Обобщенный МНК
Задача №1.Зависимость между объемом реализованной продукции X и балансовой прибылью Y предприятий одной из отраслей промышленности характеризуется данными, представленными в таблице
- В рамках степенной модели найдите регрессионную зависимость Y от X.
- Вычислите коэффициент корреляции между X и Y.
- Определите значимость регрессии для α = 0,05.
- Вычислите коэффициент детерминации R2.
| X | 1,7 | 2,2 | 8,6 | 1,3 | 3,4 | 3,9 | 4,7 | 5,8 | 3,6 | 6,4 | 7,2 |
| Y | 20 | 75 | 41 | 82 | 106 | 129 | 145 | 180 | 210 | 250 | 262 |
Задача №2. Построить модель множественной регрессии (проанализировать аномальные явления, матрицу парных коэффициентов корреляции, экономический смысл полученной модели, сравнить линейную и степенную модели.
Зависимый фактор:
У- производительность труда, (тыс. руб.)
Для модели в относительных показателях
Х1- удельный вес стоимости сырья и материалов в себестоимости продукции
Х2- удельный вес заработной платы в себестоимости продукции
Х3- фондовооруженность одного рабочего, тыс.руб./чел.
Х4- удельный вес отчислений на соц. страхования в себестоимости продукции
Х5- удельный вес расходов на подготовку и освоение производства в себестоимости продукции
Х6- электровооруженность одного рабочего, тыс. кВт./ чел.
Данные представлены в таблице 2.
Таблица 2
| № Объекта наблюдения | Y | X1 | X2 | X3 | X4 | X5 | X6 |
| 1 | 10.6 | 16,8 | 12,6 | 5,7 | 1,0 | 3,2 | 0,06 |
| 2 | 19.7 | 33,1 | 4,5 | 8,0 | 0,4 | 2,8 | 0,08 |
| 3 | 17.7 | 9,9 | 7,7 | 4,6 | 0,6 | 3,0 | 0,08 |
| 4 | 17.5 | 63,1 | 8,6 | 4,1 | 0,7 | 2,8 | 0,08 |
| 5 | 15.7 | 32,8 | 6,3 | 8,0 | 0,5 | 2,8 | 0,10 |
| 6 | 11.3 | 40,3 | 9,9 | 5,2 | 0,8 | 3,1 | 0,08 |
| 7 | 14.4 | 28,3 | 7,7 | 7,1 | 0,6 | 3,0 | 0,09 |
| 8 | 9.4 | 25,2 | 14,6 | 7,2 | 1,2 | 3,2 | 0,11 |
| 9 | 11.9 | 47,3 | 9,9 | 4,5 | 0,7 | 3,0 | 0,13 |
| 10 | 13.9 | 26,8 | 9,3 | 9,4 | 0,8 | 13,1 | 0,11 |
| 11 | 8.9 | 25,4 | 14,6 | 6,5 | 1,2 | 3,2 | 0,08 |
| 12 | 14.5 | 14,2 | 8,0 | 8,5 | 0,7 | 3,2 | 0,13 |
Билет №3
- Системы линейных одновременных уравнений. Условия идентификации.
Задача №1. Имеется 12 измерений предела прочности Z (кг/см2) при сжатии от объемного веса х (г/см2) известняка. Оценить коэффициенты модели показательного типа: у=аbх
| Х | 1,65 | 1,75 | 1,85 | 1,95 | 2,05 | 2,15 | 2,25 | 2,35 | 2,45 | 2,55 | 2,65 | 2,75 |
| у | 122,7 | 157,7 | 181,2 | 188,1 | 284,3 | 295,9 | 418,7 | 480,8 | 603,3 | 812,3 | 1093,6 | 1201,2 |
Оценить качество построенной модели
Задача №2. Пусть имеются некоторые данные об объеме реализации одного из продуктов фирмы. На основании содержательного анализа составлен перечень показателей (Объем реализации, Время, Реклама, Цена, Цена конкурента, Индекс потребит. расходов, которые предполагается включить в модель, и составлена таблица исходных данных.
С использованием надстройки «Анализ данных» решить задачу множественной регрессии. Построить пространственную модель регрессии. Результат обсудить.
| Объем реализации | Время | Реклама | Цена | Цена конкурента | Индекс потребительских расходов |
| у | х1 | х2 | х3 | х4 | х5 |
| 126 | 1 | 4 | 15 | 17 | 100 |
| 137 | 2 | 4,8 | 14,8 | 17,3 | 98,4 |
| 148 | 3 | 3,8 | 15,2 | 16,8 | 101,2 |
| 191 | 4 | 8,7 | 15,5 | 16,2 | 103,5 |
| 274 | 5 | 8,2 | 15,5 | 16 | 104,1 |
| 370 | 6 | 9,7 | 16 | 18 | 107 |
| 432 | 7 | 14,7 | 18,1 | 20,2 | 107,4 |
| 445 | 8 | 18,7 | 13 | 15,8 | 108,5 |
| 367 | 9 | 19,8 | 15,8 | 18,2 | 108,3 |
| 367 | 10 | 10,6 | 16,9 | 16,8 | 109,2 |
| 321 | 11 | 8,6 | 16,3 | 17 | 110,1 |
| 307 | 12 | 6,5 | 16,1 | 18,3 | 110,7 |
| 331 | 13 | 12,6 | 15,4 | 16,4 | 110,3 |
| 345 | 14 | 6,5 | 15,7 | 16,2 | 111,8 |
| 364 | 15 | 5,8 | 16 | 17,7 | 112,3 |
| 384 | 16 | 5,7 | 15,1 | 16,2 | 112,9 |
Билет №4
- Оценка параметров структурной формы модели. Косвенный метод наименьших квадратов.
Задача №1. Имеются данные о продаже квартир на вторичном рынке жилья.
В таблице для обозначения типа дома используются следующие обозначения: 0 – «хрущевка», 1 – панельный дом, 2 – кирпичный дом. По данным табл. построить множественную регрессию, оценивая регрессионную зависимость цены квартиры от ее полезной площади и от фиктивных переменныхD1 и D2.
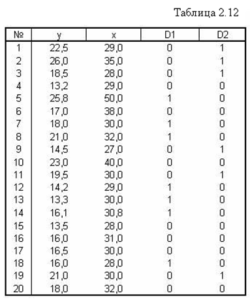
Задача №2. Зависимость между объемом реализованной продукции X и балансовой прибылью Y предприятий одной из отраслей промышленности характеризуется данными, представленными в таблице.
- В рамках линейной модели найдите регрессионную зависимость Y от X.
- Вычислите коэффициент корреляции между X и Y.
- Определите значимость регрессии для α = 0,05.
- Вычислите коэффициент детерминации R2.
| X | 1,7 | 2,2 | 8,6 | 1,3 | 3,4 | 3,9 | 4,7 | 5,8 | 3,6 | 6,4 | 7,2 |
| Y | 20 | 75 | 41 | 82 | 106 | 129 | 145 | 180 | 210 | 250 | 262 |
Билет №5
- Понятия и причины гетероскедастичности. Последствия и обнаружение гетероскедастичности.
Задача №1 У семи сотрудников предприятия собраны данные (табл. 3) об их среднемесячной зарплате (Y), возрасте (X1) и стаже работы (X2).
- С помощью метода наименьших квадратов (МНК) оценить параметры линейной модели вида y= a0+a1x1+a2x2+e, влияния возраста и стажа работы на среднемесячную зарплату;
- Рассчитать коэффициент детерминации.
| X1 | 35 | 45 | 25 | 55 | 30 | 42 | 25 |
| X2 | 5 | 10 | 3 | 12 | 1 | 8 | 2 |
| Y | 1600 | 2000 | 1450 | 2200 | 1400 | 1800 | 1 350 |
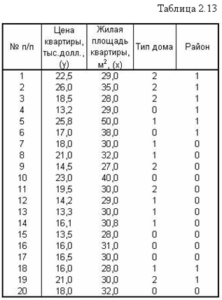
Задача №2. Исследовать воздействие на цену квартиры района, в котором она находится, а также влияние того, в доме какого типа («хрущевка», панельный, кирпичный) она находится. Использовать фиктивные переменные.
Билет №6
- Обобщенный метод наименьших квадратов в случае гетероскедастичности остатков.
Задача №1. Имеются следующие данные (условные) о сменной добыче угля на одного рабочего y(т), мощности пласта x1(м) и уровне механизации работ x2(%), характеризующие процесс добычи угля в 10 шахтах.
| № | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 8 | 11 | 12 | 9 | 8 | 8 | 9 | 9 | 8 | 12 | |
| 5 | 8 | 8 | 5 | 7 | 8 | 6 | 4 | 5 | 7 | |
| 5 | 10 | 10 | 7 | 5 | 6 | 6 | 5 | 6 | 8 |
- С помощью метода наименьших квадратов (МНК) оценить параметры линейной модели вида y= a0+a1x1+a2x2+e, влияния возраста и стажа работы на среднемесячную зарплату;
- Рассчитать коэффициент детерминации
Задача №2. По данным таблицы 1 построить уравнение множественной регрессии в естественной и стандартизованной форме.
| Объем
реализации |
Время | Реклама | Цена | Цена кон-
курента |
Индекс
потребит. расходов |
| у | х1 | х2 | х3 | х4 | х5 |
| 126
137 148 191 274 370 432 445 367 367 321 307 331 345 364 384 |
1
2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 |
4
4,8 3,8 8,7 8,2 9,7 14,7 18,7 19,8 10,6 8,6 6,5 12,6 6,5 5,8 5,7 |
15,0
14,8 15,2 15,5 15,5 16,0 18,1 13,0 15,8 16,9 16,3 16,1 15,4 15,7 16,0 15,1 |
17,0
17,3 16,8 16,2 16,0 18,0 2,02 15,8 18,2 16,8 17,0 18,3 16,4 16,2 17,7 16,2 |
100,0
98,4 101,2 103,5 104,1 107,0 107,4 108,5 108,3 109,2 110,1 110,7 110,3 111,8 112,3 112,9 |
Билет №7
- Двухшаговый и трёхшаговый метод наименьших квадратов
Задача № 1. По предприятиям региона изучается зависимость выработки продукции на одного работника (тыс. руб.) от ввода в действие новых основных фондов ( от стоимости фондов на конец года) и от удельного веса рабочих высокой квалификации в общей численности рабочих ( ).
| Номер предприятия | Номер предприятия | ||||||
| 1 | 7,0 | 3,9 | 10,0 | 11 | 9,0 | 6,0 | 21,0 |
| 2 | 7,0 | 3,9 | 14,0 | 12 | 11,0 | 6,4 | 22,0 |
| 3 | 7,0 | 3,7 | 15,0 | 13 | 9,0 | 6,8 | 22,0 |
| 4 | 7,0 | 4,0 | 16,0 | 14 | 11,0 | 7,2 | 25,0 |
| 5 | 7,0 | 3,8 | 17,0 | 15 | 12,0 | 8,0 | 28,0 |
| 6 | 7,0 | 4,8 | 19,0 | 16 | 12,0 | 8,2 | 29,0 |
| 7 | 8,0 | 5,4 | 19,0 | 17 | 12,0 | 8,1 | 30,0 |
| 8 | 8,0 | 4,4 | 20,0 | 18 | 12,0 | 8,5 | 31,0 |
| 9 | 8,0 | 5,3 | 20,0 | 19 | 14,0 | 9,6 | 32,0 |
| 10 | 10,0 | 6,8 | 20,0 | 20 | 14,0 | 9,0 | 36,0 |
- С помощью метода наименьших квадратов (МНК) оценить параметры линейной модели вида y= a0+a1x1+a2x2+e, влияния возраста и стажа работы на среднемесячную зарплату;
- Рассчитать коэффициент детерминации.
Задача 2. В табл. 1.3 представлены статистические данные о расходах на питание и душевом доходе для девяти групп семей. Рассчитайте параметры уравнения линейной, парной регрессии.
|
Номер группы |
Расход на питание ( у.д.е.) |
Душевой доход (у.д.е.) |
| 1 | 433 | 628 |
| 2 | 616 | 1577 |
| 3 | 900 | 2659 |
| 4 | 1113 | 3701 |
| 5 | 1305 | 4796 |
| 6 | 1488 | 5926 |
| 7 | 1645 | 7281 |
| 8 | 1914 | 9350 |
| 9 | 2411 | 18807 |
Билет №8
- Особенности моделирования временных рядов.
Задача 1. С помощью метода наименьших квадратов (МНК) оценить параметры линейной модели вида y= a0+a1x1+a2x2+e, влияния возраста и стажа работы на среднемесячную зарплату;
2. Рассчитать коэффициент детерминации
Задача 2. Потребление электрической энергии в учебных корпусах института приведено в таблице
Таблица 1
| Год | месяц | Потребление электроэнергии |
| 2015 | 1 | 80000 |
| 2 | 60000 | |
| 3 | 47668 | |
| 4 | 127823 | |
| 2016 | 5 | 104827 |
| 6 | 72155 | |
| 7 | 48890 | |
| 8 | 179712 | |
| 2017 | 9 | 40743 |
| 10 | 36320 | |
| 11 | 46430 | |
| 12 | 80371 | |
| 2018 | 13 | 136171 |
| 14 | 62173 | |
| 15 | 78000 | |
| 16 | 95000 |
Построить мультипликативную модель расхода электроэнергии. Оценить адекватность и точность модели. Предсказать расход электроэнергии на 2019г.
Билет №9
Задача №1. Имеются условные данные об объемах потребления электроэнергии ( ) жителями региона за 16 кварталов
| 1 | 5,8 | 9 | 7,9 |
| 2 | 4,5 | 10 | 5,5 |
| 3 | 5,1 | 11 | 6,3 |
| 4 | 9,1 | 12 | 10,8 |
| 5 | 7,0 | 13 | 9,0 |
| 6 | 5,0 | 14 | 6,5 |
| 7 | 6,0 | 15 | 7,0 |
| 8 | 10,1 | 16 | 11,1 |
Построить модели линейного и логарифмического трендов и выбрать наиболее адекватную модель. Сделать прогноз на 2 квартала вперед.
Задача 2. Зависимость между объемом реализованной продукции X и балансовой прибылью Y предприятий одной из отраслей промышленности характеризуется данными, представленными в таблице
| X | 2 | 3 | 4 | 3 | 2 | 6 | 5 | 7 | 8 | 12 | 9 |
| Y | 20 | 50 | 57 | 63 | 22 | 75 | 60 | 81 | 87 | 102 | 95 |
- В рамках полиномиальной 2 степени модели найдите регрессионную зависимость Y от X.
- Вычислите коэффициент корреляции между X и Y.
- Определите значимость регрессии для α = 0,05.
- Вычислите коэффициент детерминации R2.
Билет №10
- Нелинейная регрессия. Нелинейные модели и их линеаризация.
Задача №1. Имеются эмпирические данные о банковских вкладах- Z и уровне доходов V по 20 территориям государства. Построить регрессию Z на V (использовать линейную и нелинейную модели)
| V | 5.8 | 6.14 | 6.64 | 6.85 | 8.11 | 8.47 | 9.09 | 9.23 | 9.59 | 9.96 |
| Z | 11.8 | 12.2 | 13.1 | 14.4 | 17.5 | 18.6 | 19.1 | 19.3 | 19.8 | 18.4 |
| V | 1.01 | 1.15 | 1.91 | 2.47 | 2.66 | 2.74 | 2.93 | 4.04 | 4.50 | 4.64 |
| Z | 11.8 | 12.2 | 13.1 | 14.4 | 17.5 | 18.6 | 19.1 | 19.3 | 19.8 | 18.4 |
Выбрать наиболее адекватную модель и обосновать свой выбор
Задача №2. Построить аддитивную модель потребления электроэнергии методом «Анализ данных» в табличном процессоре Excel. . Предсказать расход электроэнергии в следующем году.
| Год | № квартала | Потребление эл/энергии |
| 1 | 6 | |
| 1 | 2 | 4,4 |
| 3 | 5 | |
| 4 | 9 | |
| 5 | 7,2 | |
| 2 | 6 | 4,8 |
| 7 | 6 | |
| 8 | 10 | |
| 9 | 8 | |
| 3 | 10 | 5,6 |
| 11 | 6,4 | |
| 12 | 11 | |
| 13 | 9 | |
| 4 | 14 | 6,6 |
| 15 | 7 | |
| 16 | 10,8 |
Билет №11
- Мультиколлинеарность. Последствия мультиколлинеарности. Способы обнаружения и избавления от мультиколлинеарности.
Задача №1. Имеется 5 измерений показаний влагомера при разной толщине образца древесины бука. Оценить коэффициенты модели степенного ряда у=ахb
| Х | 1 | 3 | 5 | 7 | 9 |
| У | 56 | 28 | 20 | 16 | 14 |
Оценить качество построенной модели.
Задача 2. Задание 9. Зависимость между объемом реализованной продукции X и балансовой прибылью Y предприятий одной из отраслей промышленности характеризуется данными, представленными в таблице.
| X | 2 | 3 | 4 | 3 | 2 | 6 | 5 | 7 | 8 | 12 | 9 |
| Y | 20 | 50 | 57 | 63 | 22 | 75 | 60 | 81 | 87 | 102 | 95 |
- В рамках полиномиальной 3степени модели найдите регрессионную зависимость Y от X.
- Вычислите коэффициент корреляции между X и Y.
- Определите значимость регрессии для α = 0,05.
- Вычислите коэффициент детерминации R2.
Билет №12
- Измерение тесноты связи между показателями. Анализ матрицы коэффициентов парной корреляции.
Задача №1 Имеется 12 измерений предела прочности Z (кг/см2) при сжатии от объемного веса х (г/см2) известняка. Оценить коэффициенты модели показательного типа: у=аbх
| Х | 1,65 | 1,75 | 1,85 | 1,95 | 2,05 | 2,15 | 2,25 | 2,35 | 2,45 | 2,55 | 2,65 | 2,75 |
| у | 122,7 | 157,7 | 181,2 | 188,1 | 284,3 | 295,9 | 418,7 | 480,8 | 603,3 | 812,3 | 1093,6 | 1201,2 |
Оценить качество построенной модели.
Задача №2. Построить мультипликативную модель потребления электроэнергии методом «Анализ данных» в табличном процессоре Excel. Предсказать расход электроэнергии в следующем году.
| Год | № квартала | Потребление эл/энергии |
| 1 | 6 | |
| 1 | 2 | 4,4 |
| 3 | 5 | |
| 4 | 9 | |
| 5 | 7,2 | |
| 2 | 6 | 4,8 |
| 7 | 6 | |
| 8 | 10 | |
| 9 | 8 | |
| 3 | 10 | 5,6 |
| 11 | 6,4 | |
| 12 | 11 | |
| 13 | 9 | |
| 4 | 14 | 6,6 |
| 15 | 7 | |
| 16 | 10,8 |
Билет №13
- Оценка качества уравнения регрессии по критерию Фишера.
Задача №1. Зависимость между объемом реализованной продукции X и балансовой прибылью Y предприятий одной из отраслей промышленности характеризуется данными, представленными в таблице
- В рамках линейной модели найдите регрессионную зависимость Y от X.
- Вычислите коэффициент корреляции между X и Y.
- Определите значимость регрессии для α = 0,05.
- Вычислите коэффициент детерминации R2.
| X | 1,7 | 2,2 | 8,6 | 1,3 | 3,4 | 3,9 | 4,7 | 5,8 | 3,6 | 6,4 | 7,2 |
| Y | 20 | 75 | 41 | 82 | 106 | 129 | 145 | 180 | 210 | 250 | 262 |
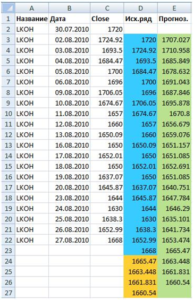
Задача №2. Построить модель авторегрессии AR1 прогнозирования курса акций Лукойла. Можете проверить полученные результаты в столбцах D и E.
Билет №14
- Анализ статистической связи экономических данных, корреляция; вычисление коэффициентов корреляции, регрессия, проверка значимости регрессионных моделей.
Задача 1. Зависимость между объемом реализованной продукции X и балансовой прибылью Y предприятий одной из отраслей промышленности характеризуется данными, представленными в таблице. В рамках логарифмической модели найдите регрессионную зависимость Y от X.
| X | 2 | 3 | 4 | 3 | 2 | 6 | 5 | 7 | 8 | 12 | 9 |
| Y | 20 | 50 | 57 | 63 | 22 | 75 | 60 | 81 | 87 | 102 | 95 |
- Вычислите коэффициент корреляции между X и Y.
- Определите значимость регрессии для α = 0,01.
- Вычислите коэффициент детерминации R2.
Задача 2. У семи сотрудников предприятия собраны данные (табл.) об их среднемесячной зарплате (Y), возрасте (X1) и стаже работы (X2).
- С помощью метода наименьших квадратов (МНК) оценить параметры линейной модели вида y= a0+a1x1+a2x2+e , влияния возраста и стажа работы на среднемесячную зарплату;
- Рассчитать коэффициент детерминации.
- Оценить качество построенной модели
| X1 | 35 | 45 | 25 | 55 | 30 | 42 | 25 |
| X2 | 5 | 10 | 3 | 12 | 1 | 8 | 2 |
| Y | 1600 | 2000 | 1450 | 2200 | 1400 | 1800 | 1 350 |
Билет №15
- Проверка качества коэффициентов многофакторных регрессионных моделей по критерию Стьюдента.
Задача №1. Имеются следующие данные (условные) о сменной добыче угля на одного рабочего y(т), мощности пласта x1(м) и уровне механизации работ x2(%), характеризующие процесс добычи угля в 10 шахтах.
| № | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 8 | 11 | 12 | 9 | 8 | 8 | 9 | 9 | 8 | 12 | |
| 5 | 8 | 8 | 5 | 7 | 8 | 6 | 4 | 5 | 7 | |
| 5 | 10 | 10 | 7 | 5 | 6 | 6 | 5 | 6 | 8 |
Задача №2. По данным таблицы 1 построить уравнение линейной регрессии в стандартизованной форме. По фактору x2.
Таблица 1.
| Объем реализации | Время | Реклама | Цена | Цена конкурента | Индекс потребит. расходов |
| у | х1 | х2 | х3 | х4 | х5 |
| 126
137 148 191 274 370 432 445 367 367 321 307 331 345 364 384 |
1
2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 |
4
4,8 3,8 8,7 8,2 9,7 14,7 18,7 19,8 10,6 8,6 6,5 12,6 6,5 5,8 5,7 |
15,0
14,8 15,2 15,5 15,5 16,0 18,1 13,0 15,8 16,9 16,3 16,1 15,4 15,7 16,0 15,1 |
17,0
17,3 16,8 16,2 16,0 18,0 2,02 15,8 18,2 16,8 17,0 18,3 16,4 16,2 17,7 16,2 |
100,0
98,4 101,2 103,5 104,1 107,0 107,4 108,5 108,3 109,2 110,1 110,7 110,3 111,8 112,3 112,9 |
Билет №16
- Модель множественной регрессии. Выбор вида модели и оценка её параметров.
Задача №1. Имеются условные данные об объемах потребления электроэнергии ( ) жителями региона за 16 кварталов. Построить линейную, экспоненциальную и логарифмическую модели методом построения линии тренда в табличном процессоре Excel. Выбрать наиболее адекватную модель.
| 1 | 5,8 | 9 | 7,9 |
| 2 | 4,5 | 10 | 5,5 |
| 3 | 5,1 | 11 | 6,3 |
| 4 | 9,1 | 12 | 10,8 |
| 5 | 7,0 | 13 | 9,0 |
| 6 | 5,0 | 14 | 6,5 |
| 7 | 6,0 | 15 | 7,0 |
| 8 | 10,1 | 16 | 11,1 |
- Задача №2. Пусть имеются некоторые данные об объеме реализации одного из продуктов фирмы. На основании содержательного анализа составлен перечень показателей (Объем реализации, Время, Реклама, Цена, Цена конкурента, Индекс потребит. расходов, которые предполагается включить в модель, и составлена таблица исходных данных. Методом построения тренда решить задачу парной регрессии. В качестве факторного признака взять расходы на рекламу. Результат обсудить.
| Объем реализации | Время | Реклама | Цена | Цена конкурента | Индекс потребительских расходов |
| у | х1 | х2 | х3 | х4 | х5 |
| 126 | 1 | 4 | 15 | 17 | 100 |
| 137 | 2 | 4,8 | 14,8 | 17,3 | 98,4 |
| 148 | 3 | 3,8 | 15,2 | 16,8 | 101,2 |
| 191 | 4 | 8,7 | 15,5 | 16,2 | 103,5 |
| 274 | 5 | 8,2 | 15,5 | 16 | 104,1 |
| 370 | 6 | 9,7 | 16 | 18 | 107 |
| 432 | 7 | 14,7 | 18,1 | 20,2 | 107,4 |
| 445 | 8 | 18,7 | 13 | 15,8 | 108,5 |
| 367 | 9 | 19,8 | 15,8 | 18,2 | 108,3 |
| 367 | 10 | 10,6 | 16,9 | 16,8 | 109,2 |
| 321 | 11 | 8,6 | 16,3 | 17 | 110,1 |
| 307 | 12 | 6,5 | 16,1 | 18,3 | 110,7 |
Билет №17
- Оценка существенности параметров линейной регрессии.
Задача 1. Зависимость между объемом реализованной продукции X и балансовой прибылью Y предприятий одной из отраслей промышленности характеризуется данными, представленными в таблице. В рамках линейной модели найдите регрессионную зависимость Y от X.
| X | 2 | 3 | 4 | 3 | 2 | 6 | 5 | 7 | 8 | 12 | 9 |
| Y | 20 | 50 | 57 | 63 | 22 | 75 | 60 | 81 | 87 | 102 | 95 |
- Вычислите коэффициент корреляции между X и Y.
- Определите значимость регрессии для α = 0,05.
- Вычислите коэффициент детерминации R2.
Задача №2. Пусть имеются некоторые данные об объеме реализации одного из продуктов фирмы. На основании содержательного анализа составлен перечень показателей (Объем реализации, Время, Реклама, Цена, Цена конкурента, Индекс потребит. расходов, которые предполагается включить в модель, и составлена таблица исходных данных. С использованием надстройки «Анализ данных» решить задачу парной регрессии. В качестве факторного признака взять расходы на рекламу. Дать оценку полученного результата.
| Объем реализации | Время | Реклама | Цена | Цена конкурента | Индекс потребительских расходов |
| у | х1 | х2 | х3 | х4 | х5 |
| 126 | 1 | 4 | 15 | 17 | 100 |
| 137 | 2 | 4,8 | 14,8 | 17,3 | 98,4 |
| 148 | 3 | 3,8 | 15,2 | 16,8 | 101,2 |
| 191 | 4 | 8,7 | 15,5 | 16,2 | 103,5 |
| 274 | 5 | 8,2 | 15,5 | 16 | 104,1 |
| 370 | 6 | 9,7 | 16 | 18 | 107 |
| 432 | 7 | 14,7 | 18,1 | 20,2 | 107,4 |
| 445 | 8 | 18,7 | 13 | 15,8 | 108,5 |
| 367 | 9 | 19,8 | 15,8 | 18,2 | 108,3 |
| 367 | 10 | 10,6 | 16,9 | 16,8 | 109,2 |
| 321 | 11 | 8,6 | 16,3 | 17 | 110,1 |
| 307 | 12 | 6,5 | 16,1 | 18,3 | 110,7 |
| 331 | 13 | 12,6 | 15,4 | 16,4 | 110,3 |
| 345 | 14 | 6,5 | 15,7 | 16,2 | 111,8 |
| 364 | 15 | 5,8 | 16 | 17,7 | 112,3 |
| 384 | 16 | 5,7 | 15,1 | 16,2 | 112,9 |
Билет №18
- Отбор факторов при построении множественной регрессии. Процедура пошагового отбора переменных.
Задача №1. Имеется 12 измерений предела прочности Z (кг/см2) при сжатии от объемного веса х (г/см2) известняка. Оценить коэффициенты модели показательного типа: у=аbх
| Х | 1,65 | 1,75 | 1,85 | 1,95 | 2,05 | 2,15 | 2,25 | 2,35 | 2,45 | 2,55 | 2,65 | 2,75 |
| у | 122,7 | 157,7 | 181,2 | 188,1 | 284,3 | 295,9 | 418,7 | 480,8 | 603,3 | 812,3 | 1093,6 | 1201,2 |
Задача 2. У семи сотрудников предприятия собраны данные (табл.) об их среднемесячной зарплате (Y), возрасте (X1) и стаже работы (X2).
- С помощью метода наименьших квадратов (МНК) оценить параметры линейной модели вида y= a0+a1x1+a2x2+e , влияния возраста и стажа работы на среднемесячную зарплату;
- Рассчитать коэффициент детерминации.
- Оценить качество построенной модели
| X1 | 35 | 45 | 25 | 55 | 30 | 42 | 25 |
| X2 | 5 | 10 | 3 | 12 | 1 | 8 | 2 |
| Y | 1600 | 2000 | 1450 | 2200 | 1400 | 1800 | 1 350 |
Билет №19
- Понятия регрессионного анализа: зависимые и независимые переменные. Оценка качества уравнения регрессии
Задача №1. Имеется 5 измерений показаний влагомера при разной толщине образца древесины бука. Найти коэффициенты модели степенного ряда у=ахb . Оценить качество построенной модели.
| Х | 1 | 3 | 5 | 7 | 9 |
| У | 56 | 28 | 20 | 16 | 14 |
Задача №2. Построить аддитивную модель потребления электроэнергии методом «Анализ данных» в табличном процессоре Excel. . Предсказать расход электроэнергии в следующем году. Оценить качество модели.
| Год | № квартала | Потребление эл/энергии |
| 1 | 6 | |
| 1 | 2 | 4,4 |
| 3 | 5 | |
| 4 | 9 | |
| 5 | 7,2 | |
| 2 | 6 | 4,8 |
| 7 | 6 | |
| 8 | 10 | |
| 9 | 8 | |
| 3 | 10 | 5,6 |
| 11 | 6,4 | |
| 12 | 11 | |
| 13 | 9 | |
| 4 | 14 | 6,6 |
| 15 | 7 | |
| 16 | 10,8 |
Билет №20
- Типы экономических данных, используемых в эконометрических исследованиях. Классификация эконометрических моделей. Основные этапы построения эконометрических моделей
Задача №1. По 20 предприятиям региона изучается зависимость выработки продукции на одного работника (тыс. руб.) от ввода в действие новых основных фондов (% от стоимости фондов на конец года) и от удельного веса рабочих высокой квалификации в общей численности рабочих (%).
| Номер предприятия | Номер предприятия | ||||||
| 1 | 6 | 3,6 | 9 | 11 | 9 | 6,3 | 21 |
| 2 | 6 | 3,6 | 12 | 12 | 11 | 6,4 | 22 |
| 3 | 6 | 3,9 | 14 | 13 | 11 | 7 | 24 |
| 4 | 7 | 4,1 | 17 | 14 | 12 | 7,5 | 25 |
| 5 | 7 | 3,9 | 18 | 15 | 12 | 7,9 | 28 |
| 6 | 7 | 4,5 | 19 | 16 | 13 | 8,2 | 30 |
| 7 | 8 | 5,3 | 19 | 17 | 13 | 8 | 30 |
| 8 | 8 | 5,3 | 19 | 18 | 13 | 8,6 | 31 |
| 9 | 9 | 5,6 | 20 | 19 | 14 | 9,5 | 33 |
| 10 | 10 | 6,8 | 21 | 20 | 14 | 9 | 36 |
- С помощью метода наименьших квадратов (МНК) оценить параметры линейной модели вида y= a0+a1x1+a2x2+e, влияния возраста и стажа работы на среднемесячную зарплату;
- Рассчитать коэффициент детерминации
Задача 2. В табл. 1.3 представлены статистические данные о расходах на питание и душевом доходе для девяти групп семей. Рассчитайте параметры уравнения степенной, парной регрессии.
| Номер группы | Расход на питание ( у.д.е.) | Душевой доход (у.д.е.) |
| 1 | 433 | 628 |
| 2 | 616 | 1577 |
| 3 | 900 | 2659 |
| 4 | 1113 | 3701 |
| 5 | 1305 | 4796 |
| 6 | 1488 | 5926 |
| 7 | 1645 | 7281 |
| 8 | 1914 | 9350 |
| 9 | 2411 | 18807 |
Билет №21
Задача №1. Имеется 5 измерений показаний влагомера при разной толщине образца древесины бука. Оценить значимость коэффициентов модели степенного ряда у=ахb. Оценить качество построенной модели.
| Х | 1 | 3 | 5 | 7 | 9 |
| У | 56 | 28 | 20 | 16 | 14 |
Задача №2. Построить мультипликативную модель потребления электроэнергии методом «Анализ данных» в табличном процессоре Excel. . Предсказать расход электроэнергии в следующем году. Оценить качество модели.
| Год | № квартала | Потребление эл/энергии |
| 1 | 6 | |
| 1 | 2 | 4,4 |
| 3 | 5 | |
| 4 | 9 | |
| 5 | 7,2 | |
| 2 | 6 | 4,8 |
| 7 | 6 | |
| 8 | 10 | |
| 9 | 8 | |
| 3 | 10 | 5,6 |
| 11 | 6,4 | |
| 12 | 11 | |
| 13 | 9 | |
| 4 | 14 | 6,6 |
| 15 | 7 | |
| 16 | 10,8 |
Билет №22
- Анализ статистической связи экономических данных, корреляция; вычисление коэффициентов корреляции, регрессия, проверка значимости регрессионных моделей.
Задача №1. Имеется 12 измерений предела прочности Z (кг/см2) при сжатии от объемного веса х (г/см2) известняка. Найти коэффициенты модели показательного типа: у=аbх. Оценить точность модели.
| Х | 1,65 | 1,75 | 1,85 | 1,95 | 2,05 | 2,15 | 2,25 | 2,35 | 2,45 | 2,55 | 2,65 | 2,75 |
| у | 122,7 | 157,7 | 181,2 | 188,1 | 284,3 | 295,9 | 418,7 | 480,8 | 603,3 | 812,3 | 1093,6 | 1201,2 |
Задача №2. Изучается влияние стоимости основных и оборотных средств на величину валового дохода торговых предприятий.
- Определить парные коэффициенты корреляции и оценить влияние факторов на результат.
- Построить модель множественной регрессии и сделать выводы о влиянии стоимости основных и оборотных средств на величину валового дохода торговых предприятий.
- Оценить адекватность модели.
| Номер предприятия | Валовой доход за год млн. руб | Среднегодовая стоимость млн.руб | |
| Основных фондов | Оборотных фондов | ||
| 1 | 203 | 118 | 105 |
| 2 | 63 | 28 | 56 |
| 3 | 45 | 17 | 54 |
| 4 | 113 | 50 | 63 |
| 5 | 88 | 102 | 50 |
| 6 | 121 | 56 | 38 |
| 7 | 110 | 116 | 54 |
| 8 | 56 | 124 | 42 |
| 9 | 80 | 114 | 36 |
| 10 | 237 | 154 | 106 |
| 11 | 160 | 115 | 88 |
| 12 | 75 | 98 | 46 |
Билет №23
- Методы исключения тенденции.
Задача №1. Имеются эмпирические данные о банковских вкладах- Z и уровне доходов V по 20 территориям государства. Построить регрессию Z на V (использовать линейную и степенную модели. Выбрать наиболее адекватную модель и обосновать свой выбор.
| V | 5.8 | 6.14 | 6.64 | 6.85 | 8.11 | 8.47 | 9.09 | 9.23 | 9.59 | 9.96 |
| Z | 11.8 | 12.2 | 13.1 | 14.4 | 17.5 | 18.6 | 19.1 | 19.3 | 19.8 | 18.4 |
| V | 1.01 | 1.15 | 1.91 | 2.47 | 2.66 | 2.74 | 2.93 | 4.04 | 4.50 | 4.64 |
| Z | 11.8 | 12.2 | 13.1 | 14.4 | 17.5 | 18.6 | 19.1 | 19.3 | 19.8 | 18.4 |
Задание 2. По 20 предприятиям региона изучается зависимость выработки продукции на одного работника (тыс. руб.) от ввода в действие новых основных фондов (% от стоимости фондов на конец года) и от удельного веса рабочих высокой квалификации в общей численности рабочих (%) (смотри таблицу своего варианта).
| Номер предприятия | Номер предприятия | ||||||
| 1 | 6 | 3,6 | 9 | 11 | 9 | 6,3 | 21 |
| 2 | 6 | 3,6 | 12 | 12 | 11 | 6,4 | 22 |
| 3 | 6 | 3,9 | 14 | 13 | 11 | 7 | 24 |
| 4 | 7 | 4,1 | 17 | 14 | 12 | 7,5 | 25 |
| 5 | 7 | 3,9 | 18 | 15 | 12 | 7,9 | 28 |
| 6 | 7 | 4,5 | 19 | 16 | 13 | 8,2 | 30 |
| 7 | 8 | 5,3 | 19 | 17 | 13 | 8 | 30 |
| 8 | 8 | 5,3 | 19 | 18 | 13 | 8,6 | 31 |
| 9 | 9 | 5,6 | 20 | 19 | 14 | 9,5 | 33 |
| 10 | 10 | 6,8 | 21 | 20 | 14 | 9 | 36 |
- С помощью метода наименьших квадратов (МНК) оценить параметры линейной модели вида y= a0+a1x1+a2x2+e , влияния возраста и стажа работы на среднемесячную зарплату;
- Рассчитать коэффициент детерминации. Дать экономическую интерпретацию полученного результата.
Билет №24
- Автокорреляция в остатках. Критерий Дарбина-Уотсона.
Задача 1. Метод отклонений от тренда. Включение в модель регрессии фактора времени.
Задача 1. Имеются следующие данные (условные) о сменной добыче угля на одного рабочего y(т), мощности пласта x1(м) и уровне механизации работ x2(%), характеризующие процесс добычи угля в 10 шахтах.
| № | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 8 | 11 | 12 | 9 | 8 | 8 | 9 | 9 | 8 | 12 | |
| 5 | 8 | 8 | 5 | 7 | 8 | 6 | 4 | 5 | 7 | |
| 5 | 10 | 10 | 7 | 5 | 6 | 6 | 5 | 6 | 8 |
- С помощью метода наименьших квадратов (МНК) оценить параметры линейной модели вида y= a0+a1x1+a2x2+e , влияния возраста и стажа работы на среднемесячную зарплату;
- Рассчитать коэффициент детерминации
Задача №2.. По 20 предприятиям региона изучается зависимость выработки продукции на одного работника (тыс. руб.) от ввода в действие новых основных фондов ( от стоимости фондов на конец года) и от удельного веса рабочих высокой квалификации в общей численности рабочих ( ).
| Номер предприятия | Номер предприятия | ||||||
| 1 | 7,0 | 3,9 | 10,0 | 11 | 9,0 | 6,0 | 21,0 |
| 2 | 7,0 | 3,9 | 14,0 | 12 | 11,0 | 6,4 | 22,0 |
| 3 | 7,0 | 3,7 | 15,0 | 13 | 9,0 | 6,8 | 22,0 |
| 4 | 7,0 | 4,0 | 16,0 | 14 | 11,0 | 7,2 | 25,0 |
| 5 | 7,0 | 3,8 | 17,0 | 15 | 12,0 | 8,0 | 28,0 |
| 6 | 7,0 | 4,8 | 19,0 | 16 | 12,0 | 8,2 | 29,0 |
| 7 | 8,0 | 5,4 | 19,0 | 17 | 12,0 | 8,1 | 30,0 |
| 8 | 8,0 | 4,4 | 20,0 | 18 | 12,0 | 8,5 | 31,0 |
| 9 | 8,0 | 5,3 | 20,0 | 19 | 14,0 | 9,6 | 32,0 |
| 10 | 10,0 | 6,8 | 20,0 | 20 | 14,0 | 9,0 | 36,0 |
- С помощью метода наименьших квадратов (МНК) оценить параметры линейной модели вида y= a0+a1x1+a2x2+e , влияния возраста и стажа работы на среднемесячную зарплату;
- Рассчитать коэффициент детерминации
Билет №25
- Проверка качества коэффициентов многофакторных регрессионных моделей по критерию Стьюдента.
Задача №1. Имеются следующие данные (условные) о сменной добыче угля на одного рабочего y(т), мощности пласта x1(м) и уровне механизации работ x2(%), характеризующие процесс добычи угля в 10 шахтах.
| № | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 8 | 11 | 12 | 9 | 8 | 8 | 9 | 9 | 8 | 12 | |
| 5 | 8 | 8 | 5 | 7 | 8 | 6 | 4 | 5 | 7 | |
| 5 | 10 | 10 | 7 | 5 | 6 | 6 | 5 | 6 | 8 |
Задача №2. По данным таблицы 1 построить уравнение линейной регрессии в стандартизованной форме. По фактору x1.
Таблица 1.
| Объем реализации | Время | Реклама | Цена | Цена конкурента | Индекс потребит. расходов |
| у | х1 | х2 | х3 | х4 | х5 |
| 126
137 148 191 274 370 432 445 367 367 321 307 331 345 364 384 |
1
2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 |
4
4,8 3,8 8,7 8,2 9,7 14,7 18,7 19,8 10,6 8,6 6,5 12,6 6,5 5,8 5,7 |
15,0
14,8 15,2 15,5 15,5 16,0 18,1 13,0 15,8 16,9 16,3 16,1 15,4 15,7 16,0 15,1 |
17,0
17,3 16,8 16,2 16,0 18,0 2,02 15,8 18,2 16,8 17,0 18,3 16,4 16,2 17,7 16,2 |
100,0
98,4 101,2 103,5 104,1 107,0 107,4 108,5 108,3 109,2 110,1 110,7 110,3 111,8 112,3 112,9 |




